Treble loss with volume roll-off
-
Hi,
it's commonly known that most electric guitars lose treble when you roll off volume, and there's plenty of modding descriptions around, involving capacitors in parallel with the volume pot for example. I've always wondered why even modern guitars rarely have this compensation from factory. But I'm even more curious to understand exactly why the volume pot acts like a low-pass filter component together with the pickups, the cable and the amp's input impedance. Is there anyone who could explain what's going on?
Cheers/Par -
Hello Parca,
Interesting topic! It was quite time ago I played around with the electric guitars electronics. I have definitely noticed the volume pots impact of the frequency response but never asked myself the specific question, how and why. My first intuitive answer would be that it easily can be explained by the common RLC circuit. I will try to do a simulation and see if I can come up with an easy and obvious answer or if it this phenomena needs a more complicated explanation. @parca, is your experience that the volume pot always acts like a lowpass filter or have you noticed the opposite?
Does anyone already know the answer and want to spare me some time? :pray:
-
@LarssonGuitars Thanks for your reply - it's definitely an RLC issue somehow, but strangely enough a friend and I did some modeling and came to the opposite results, i e there's a treble boost as you increase the resistance. (I have a pic but I'm not allowed to upload it (?)) .
Knowing why isn't going to help my playing, just my peace of mind :-)
Cheers
-
We will look into the uploading issue. However, I have now made a simulation test according to the setup below. I used 250k potentiometers both for the volume and tone control.
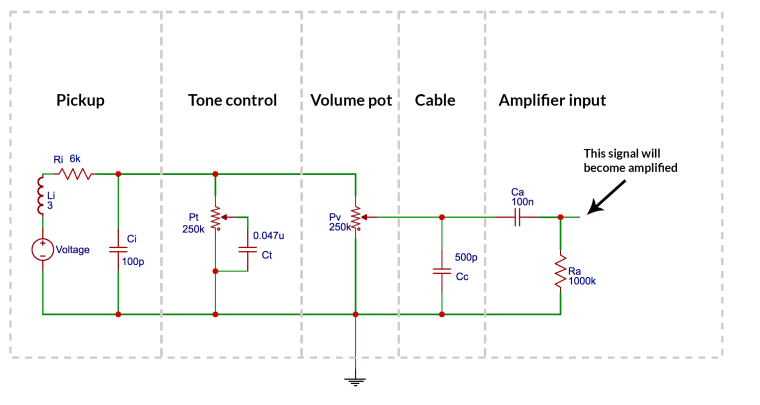
And here comes my simulation results with full volume and full tone (low filtering).
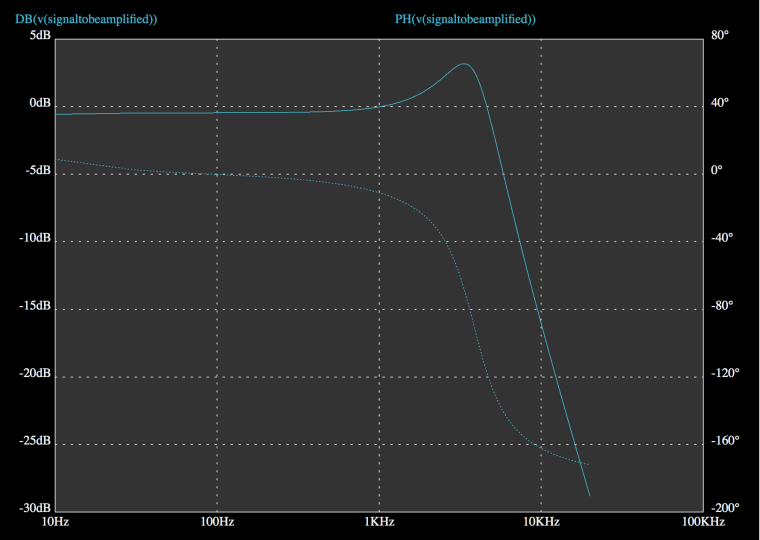
When we use "no" filtering and maximum volume the frequency response has a cut-off frequency of 5.4kHz.
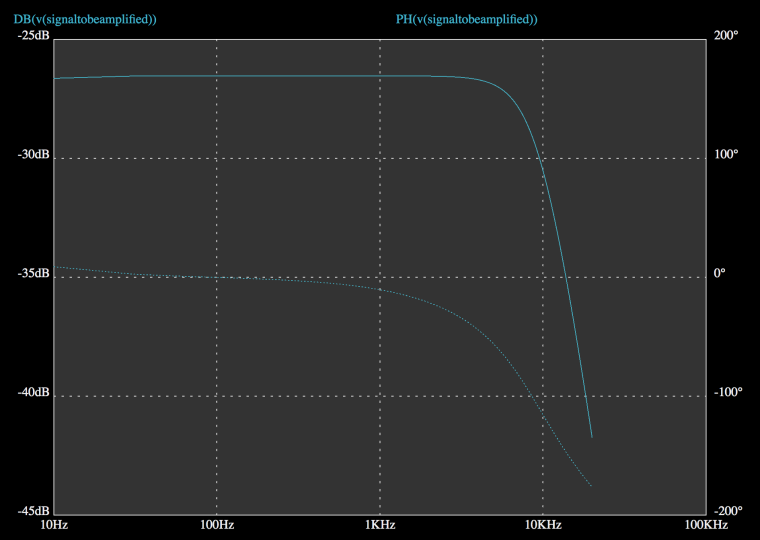
So, lets turn the tone knob to zero (full filtering). Now we have a low pass filtering effect with a cutoff frequency of approximately 600Hz and a small peak of about 350Hz. Everything looks like expected in the graph below.
Full volume and zero tone (max filtering).
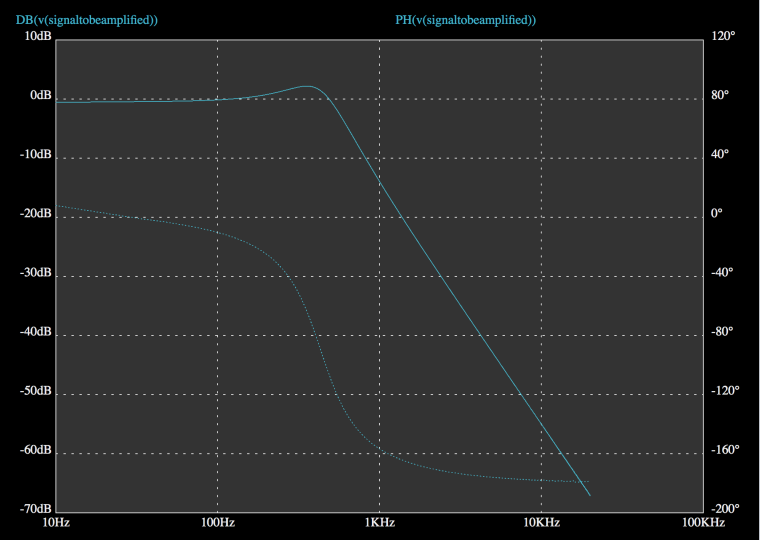
Now to the interesting question what happens when we turn back the tone pot and reduce the volume.
5% Volume and full tone (low filtering)
Oh! The cutoff frequency increases to 9kHz. Does this mean that the result would be an increase of treble and that there is something wrong with the simulation? I am not sure and I need to look into this deeper.
Compared to the first figure the frequency response is quite flat before 8k. In the first graph there is a peak between 1k and 4k with its center at 3.6k. That means all partials in that range will be up to 3dB louder when we use full volume.
Lets look into the guitars treble range. The 1st string's (E4) partials are:
f0 = 329.6 Hz
f1 = 659.3 Hz
f2 = 988.9 Hz
f3 = 1318.5 Hz
f4 = 1648.1 Hz
f5 = 1977.8 Hz
f6 = 2307.4 Hz
f7 = 2637.0 Hz
f8 = 2966.6 Hz
f9 = 3296.3 Hz
f10 = 3625.9 Hz
f12 = 3625.9 Hz
f13 = 4285.2 Hz
f14 = 4614.8 Hz
......
The second to the 14th harmonic is actually louder when we play with full volume. @parca, do you think this could explain the phenomena? Did you get similar results when simulating? -
Hello,
I have now made a practical test with a guitar and I have been able to verify some of the reasoning above. At first I made a subjective listening test both while playing the guitar but also with a generated white noise signal (through the pickup's magnetic field).
I was a little bit surprised when I generated the white noise and was lowering the volume. The noise sounded much more linear but I also perceived a treble increase. You can listen here:
Noise - Full volume
Noise - with volume roll-offDoes this mean an increase in treble? Let's look at the frequency response:

The frequency response when using full volume is represented by the red graph and the the yellow graph is when the volume knob is turned from 10 to 9.
When reducing volume the high treble range stays the same, i.e we get relatively more treble, as we could hear in the noise recording. However, the greatest difference is seen in the 1.8-4.2kHz where we loose amplitude when lowering the volume.
When playing the guitar I noticed two things when reducing the volume. I was able to verify the loss of perceived treble and clarity but I also noticed a loss in attack and dynamic range. The later is rather explained by the function of the amplifier. How is this possible? I had a hypothesis in the earlier post regarding the guitar's bandwidth and a guess that the first harmonics were more important to the perceived treble than the increase of cut off frequency. You can listen here:
E4 - Full Volume - normalised
E4 - with volume roll-off - normalisedHere comes the partials for the audio above.
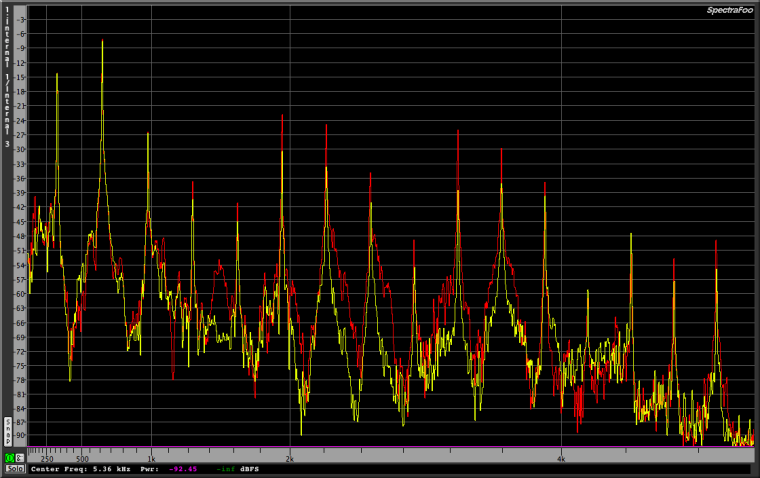
Full volume is represented by red and when normalising the signal it is quite clear that we loose treble when reducing the volume.
I am pretty confident that there is not anything wrong with the simulation and this explanation. However, this results might change from guitar to guitar and setup due to variations in inductance, impedance, and capacitance. Also, my reasoning is not an exact explanation and answer to the question; why. This is just a verification to the phenomena. To fix this (if it is considered as an issue) we have to look into why the resistor in combination with the other filter parameters impacts the ~2-4kHz range.
I used a free online software to make the simulation and I will make the project shareable. I'll come back with a link soon...
Cheers
-
I have now made the source public:
The source files at google drive
Please help to add the different fixes, simulate and make the result public!
Kind regards,
Johannes -
First of all, thanks for all the effort to research and model this!
A friend of mine did some modeling as well, and came to the conclusion that there should be a treble increase, rather than the perceived decrease:
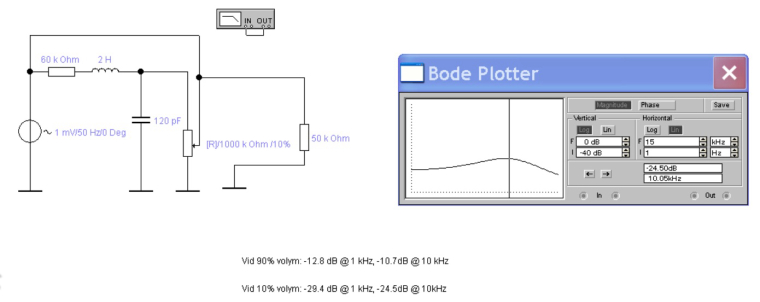
Even though the exact values differ from your (probably more correct) model, the effect is clear.So, what could we really conclude from all this? That our models are too simplistic? It seems like they contradict your empirical tests? One indication of the complexity is the fact that in your real recording example, the 12th and 13th component is really louder in the rolled-off case, right?
Thanks
